基于矩阵补全的缺失AS链路预测方法

互联网域间拓扑是指由许多自治域（Autonomous System）和连接AS的边所构成的连接图。尽管近二十年来许多研究工作致力于测量域间拓扑，互联网中仍有大量域间链路尚未被观测到^[1][2]，本文称之为缺失AS链路。现有缺失链路预测研究常关注社交网络^[3-4]、生物网络^[5]、推荐系统^[6]等场景，而目前学术界中有关缺失AS链路预测的研究工作是比较少的。自治域之间是否建立BGP连接受到多种复杂因素的影响，例如政治因素、经济因素等，这使得通用的AS链路预测方法或者为其他场景设计的链路预测方法难以很好地解决AS链路预测问题。因此，本文致力于设计一个高性能的域间缺失链路预测方法。观察发现，已有域间拓扑测量工作观察到的AS路径中不仅包含显式AS连接信息，而且还包含了大量的隐式连接信息，这为缺失AS链路预测提供了机会。因此，本文将缺失AS链路预测问题表述为从一组测量到的AS路径中学习以补全互联网域间拓扑数据，该问题适合被建模为矩阵补全问题。虽然之前有研究针对其他场景设计了矩阵补全方法用于确定图中的缺失链路^[7-10]，但是这些方法要么学习能力有限，难以应对AS路径所反映的复杂约束，要么没有融合有关自治域对等互连的实践知识，无法很好地解决本文的问题。为此，本文提出了一种基于AS辅助信息以及广义矩阵分解框架的矩阵补全方法，即SGMF（Side-information Assisted Generalized Matrix Factorization Model Based Matrix Completion Method），专门用于预测互联网中的缺失AS链路。该方法不仅继承了广义矩阵分解模型（Generalized Matrix Factorization Model，简称GMF）^[9]中神经网络所赋予的强大的学习能力，而且融入了大量与域间拓扑和路由相关的有价值的辅助信息，因此可以从多源数据中学习到更具表达能力的隐向量，实现出色的链路预测效果。实验结果表明，相比于其他先进的矩阵补全方法，SGMF可以实现高达0.834的AUC值，将域间缺失链路预测性能提升17%至44%。

缺失AS链路预测问题可以表述为在给定一组观察到的AS路径的情况下，预测缺失AS链路可能处于的位置。具体而言，本文定义了一个AS跳数矩阵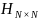来保存AS路径中包含的丰富信息，其中𝑁表示在这些路径中出现的自治域的数量。如果至少有一条AS路径经过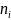AS到达AS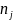，矩阵𝑯中第𝑖行第𝑗列的元素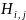将会记录这两个AS之间的最短跳数距离，否则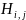将被标记为未知。通过记录AS路径所能观察到的部分AS之间的最短跳数距离，矩阵包含了大量建立在完整域间拓扑上的路由约束信息。互联网中共享的拓扑和路由约束使得AS之间的最短跳数距离通常具有较强的相关性，这意味着AS跳数矩阵应该是一个低秩矩阵，因此可以应用矩阵补全方法来借助矩阵𝑯中已知的跳数距离恢复所有未知的跳数距离。

在得到完整的AS跳数矩阵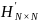之后，本文利用它来预测互联网规模的缺失AS链路。一种简单的方法是根据阈值将恢复的跳数距离划分为两类。通过假设AS之间的跳数距离与他们之间存在链路的可能性成反比，本文利用恢复的跳数矩阵𝑯′来预测一个完整的AS连接矩阵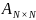，其中如果跳数矩阵元素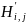大于阈值𝑇，则对应的连接矩阵元素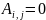（即表示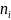AS和AS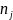之间不存在链路），否则对应的连接矩阵元素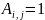（即表示AS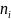和AS之间存在链路）。借助预测得到的连接矩阵𝑨，可以观察到互联网域间拓扑的缺失部分。

根据矩阵补全的相关基础理论，只有低秩矩阵才能被准确地恢复^[11]。本节将介绍AS跳数矩阵的低秩特性，以证明矩阵补全方法的可行性。考虑到仅根据少量矩阵元素难以正确估计AS跳数矩阵的秩，本节借助经典的域间路由模型^[12]模拟得到了一个完整的AS跳数矩阵，该矩阵能够在一定程度上反映真实世界的互联网路由。借助奇异值分解（Singular Value Decomposition，简称SVD）^[11]算法分析发现，前100个奇异值就能捕获𝑺中98.8%的信息量，这表明AS跳数矩阵具有低秩特性。

低秩特性使得研究人员有机会利用部分已知的AS跳数矩阵元素来估计所有未知的跳数矩阵元素。如果本节采用传统的矩阵分解（Matrix Factorization，简称MF）方法来补全秩为𝑅的AS跳数矩阵𝑯，它们会将矩阵中每一行所表示的AS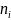以及每一列所表示的AS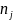分别映射到相应的隐向量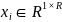和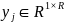，使得这些隐向量的内积尽可能地匹配已知的跳数矩阵元素。在将AS映射到相应的隐向量之后，每个未知的跳数矩阵元素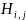等于其对应的隐向量的内积。问题在于这种传统的矩阵分解方法仅将跳数距离视为AS隐向量之间的线性组合，而实际情况下，隐向量之间的交互比这更加复杂。为了解决内积学习能力有限的问题，研究人员^[9]提出了一种广义矩阵分解方法GMF，该方法利用神经网络代替内积，增强了学习能力。虽然GMF可以用来捕获AS隐向量与跳数距离之间的复杂关系，但是该方法并没有整合任何有价值的辅助信息，难以学习更具表达能力的隐向量。本节展示了有关构建AS辅助信息的见解，并提出了基于辅助信息和GMF的矩阵补全方法SGMF，该方法将多源AS辅助信息整合到GMF模型中，显著提升了AS链路预测的性能。

2.1 多源辅助信息设计

互联网中有许多与域间拓扑和路由相关的信息，例如AS的流量特征、AS对等策略等，这些信息对于预测缺失AS链路是非常有价值的。基于对互联网对等实践的理解，本文仔细选择了如下所示的AS特征来作为辅助信息。

AS层次特征：AS层次表示自治域在互联网层次结构中的位置。通常情况下，位于相同或相近层次的自治域之间更容易建立BGP对等互连关系。因此，本节构建了一个用于记录AS层次类型的特征，其中层次类型包括顶级集团（此类AS没有服务提供商）、高层次（此类AS是顶级集团内自治域的客户且度数大于100）、低层次（此类AS不属于顶级集团、高层次或存根层）、存根层（此类AS没有客户）。

流量信息特征：AS的流量信息特征，即整体流量特征和流量比率特征，也是影响域间互连的重要因素。本节根据整体流量大小将其划分为18个级别，并基于此构建了一个用于记录AS流量级别的整体流量特征。至于流量比率，本节将其划分为五种类别：重度传出、传出为主、传出流入平衡、流入为主、重度流入。流量比率特征主要负责记录AS的流量比率属于上述哪一类别。当然，获取自治域的流量信息并不容易，好在运营商自愿在PeeringDB中共享这些信息。本节将从PeeringDB中收集自治域的流量信息特征。

对等策略特征：AS的对等策略特征，包括一般对等政策特征、多地点要求特征、流量比率要求特征以及合同要求特征，将会决定它与哪些自治域建立对等互连。例如，AS的一般对等政策通常分为开放（如果可行就建立对等互连）、选择性（在一些附加约束下建立对等互连）、限制（仅在必要时建立对等互连）。这些对等策略特征对于预测缺失AS链路也是有帮助的，而且可以从PeeringDB中采集到。

地理覆盖范围特征：两个AS的地理覆盖范围是否重叠也可能会影响BGP连接的建立。因此，本节还引入了地理覆盖范围特征，用于记录自治域在PeeringDB中共享的地理范围信息，包括全球性、区域性或者更具体的区域，例如北美、亚太等。

AS类型特征：该特征考虑了AS业务类型对域间拓扑和路由的影响。目前主要存在三种不同类型的AS：（1）提供内容托管和分发的AS；（2）提供传输或者接入服务的AS；（3）除了上述类型的AS之外，还有一些位于互联网边缘的各种组织、大学以及公司的AS。本节从CAIDA公布的AS分类数据集中采集自治域的业务类型特征。

虽然PeeringDB包含的信息并不完整而且可能会存在一些错误，且CAIDA公布的AS分类数据集也并不完全准确，但是本节设计的基于神经网络的SGMF方法仍然可以从多源数据中学习到许多有价值的信息。正如后续评估结果所示，这些AS辅助信息对于提升跳数矩阵补全性能以及缺失链路预测性能而言都是非常有效的。

2.2 SGMF框架设计

本节将上述AS辅助信息整合到GMF框架中，提出了一种基于辅助信息以及神经网络架构的矩阵补全方法SGMF，以学习更具表达能力的隐向量。

图1展示了SGMF方法的基本框架。该框架中输入层是由AS跳数矩阵中每一行（列）所表示的AS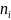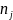（）的独热编码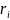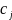（）和该AS对应的特征独热编码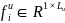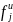（）构成的，其中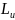表示第𝑢个特征包含的类别总数。例如，AS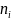位于互联网层次结构中的顶级集团，其对应的AS层次特征的独热编码表示为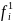= [1, 0, 0, 0]。输入层之上是嵌入层，该层主要负责将每个稀疏的独热编码映射到稠密的嵌入向量。接着，本节将行（列）AS嵌入向量以及该AS对应的特征嵌入向量拼接在一起，构建了一个信息含量丰富的行（列）AS隐向量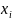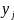（）。随后，以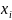和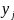为输入，SGMF借助GMF模型中的两层神经网络来估计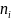AS和AS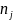之间的跳数距离。神经网络中第一层映射函数如下：

其中∘表示计算两个向量的元素积。计算得到的向量将被输入到神经网络的输出层，用于估计跳数距离：

其中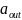表示激活函数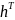，表示输出层的权重，该权重允许调整AS隐向量不同维度对于跳数距离估计的影响。SGMF方法采用线性整流函数（该函数适用于稀疏数据且能使模型不容易过拟合^[9]）来作为，并且从训练数据中学习参数𝒉。与传统矩阵分解方法所采用的内积相比，上述神经网络架构使得SGMF具有非线性表达能力、学习能力更强。

图1 SGMF框架

之所以采用两层神经网络而非采用机器学习算法或者深层神经网络，是因为它更适用于本章的场景。一方面，神经网络通常具有更强大的学习能力并且能从嘈杂的多源数据中学习到有价值的信息，相较之下，机器学习算法的学习能力有限。另一方面，AS隐向量与跳数距离之间的关系尚未复杂到需要用深度神经网络建模的程度，因此本节采用两层神经网络以避免过拟合。

接下来，本文将进行一系列的实验来证明SGMF方法的有效性。

3.1 实验设置

数据集：Routeviews以及RIPE RIS共部署了1,134个探针用于采集BGP路由数据。本节从这些探针观察到的BGP路由表快照（2021年3月29日）中提取到了一组AS路径数据。该AS路径数据集共包含72,034个自治域，因此需要构建一个𝑁×𝑁（其中N= 72,034）的AS跳数矩阵𝑯来记录这些AS路径信息。根据上述1.1节描述的方法对矩阵𝑯进行赋值后，发现该AS跳数矩阵极不完整，包含了少量（1.46 × 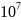个）已知矩阵元素和大量（5.17 ×个）未知矩阵元素。为了补全上述跳数矩阵进而预测缺失AS链路，本文提出的SGMF方法还需要一些AS辅助信息数据集。为此，本节利用上述BGP路由表快照计算得到AS的层次特征，并CAIDA公布的AS分类数据集中采集AS的类型特征（2020年7月1日），接着从PeeringDB中采集AS的流量信息、对等策略以及地理覆盖范围等特征（2021年4月9日）。

评估指标：本节采用RMSE（Root Mean Squared Error）和AUC来分别评估AS跳数矩阵补全的整体性能以及缺失链路预测的整体性能。AUC值等于分类器对一组随机抽取的正样本和负样本进行正确排序的概率，反映了分类器在区分正负样本方面的能力。此外，本节采用TPR以及FPR来评估缺失链路预测结果在指导拓扑测量方面的性能表现。TPR指的是全球域间拓扑未知区域内真实存在的链路中被正确预测的比例，可以衡量在预测链路的指导下执行测量所能获得的收益。FPR则指的是全球域间拓扑未知区域内实际并不存在的链路中被错误预测的比例，可以衡量消耗在非必要测量上的资源开销。TPR越高，FPR越低，意味着预测结果在指导高效拓扑测量方面的性能表现越好。

评估方法：考虑到未知AS跳数距离以及缺失AS链路主要是探针稀缺所导致的，本节将Routeviews以及RIPE RIS部署的1,134个探针随机拆分为两个集合：𝕋（包含85%的探针，用于训练）和𝕍（包含15%的探针，用于测试）。本节首先基于𝕋中探针观察到的AS路径训练得到一个SGMF模型，接着计算该模型在𝕍中探针所独有观察到的数据上的性能指标，以近似估计该模型在预测全球域间拓扑未知区域上的性能表现。上述评估方法目前已被广泛应用于路由推断、链路预测等相关研究领域。

展开来讲，本节根据𝕋中探针观察到的AS路径构建一个AS跳数矩阵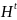，并将其用作训练集。为了评估训练好的SGMF模型在AS跳数矩阵补全方面的性能，本节借助𝕍中探针观察到的AS路径构建AS跳数矩阵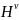，并将其中独有的跳数矩阵元素（该元素在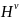中是已知的但在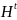中是未知的）添加到跳数距离测试集中。此外，评估SGMF模型在预测缺失AS链路方面的性能需要标注的正负样本。然而，获取标注的负样本是非常困难的，因为研究人员很难区分到底是不存在链路还是由于数据有限尚未观察到存在的链路。为了应对这一问题，本节假设若大量AS路径观察到某两个AS之间的最短跳数距离大于1，则认为它们之间往往不存在链路。基于此，本节检查了矩阵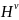包含的独有AS连接信息，并将其中的正样本（该元素在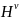中的值为1但在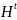中是未知的）和负样本（该元素在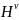中的值大于1但在中是未知的）添加到AS链路测试集中。

本节对1,134个探针进行了二十次随机拆分，并重复上述过程创建了二十组训练集和测试集用于后续进行交叉验证。为了减少数据拆分所引入的不确定性，本节将模型在多个测试集上的评估结果的均值看作是最终的性能评估结果。

超参数调整：本节将特征嵌入向量的维度设置为与特征输入向量的维度相同。至于SGMF模型中其他的超参数（例如学习率、批量大小、AS嵌入向量维度等），本节进行了超参数调整以确定最佳的超参数组合方式。具体而言，本节分别将学习率、批量大小、AS嵌入向量维度的候选参数列表设置为[0.0001, 0.0005, 0.001, 0.005]、[64, 128, 256]、[50, 100, 200]。借助随机创建的一组训练集和测试集，本节训练了一系列具有不同超参数组合方式的SGMF模型并对这些模型在AS链路测试集上的AUC性能进行了评估。观察发现，当学习率设为0.0001，批量大小设为128，AS嵌入向量维度设为50时，训练好的SGMF模型在测试集上的性能表现是最优的。

3.2 矩阵补全算法性能对比

本节将SGMF与缺乏辅助信息的GMF以及传统的基于矩阵分解的补全方法进行比较，证明了SGMF方法的有效性。由于Funk矩阵分解方法（Funk Matrix Factorization Method，简称Funk MF^[16]）和非负矩阵分解方法（Nonnegative Matrix Factorization Method，简称NMF^[17]）常用于解决矩阵补全问题^[18]，本节选择将它们作为对比基准。Funk MF采用随机梯度下降算法将矩阵的行和列分别映射到相应的隐向量，从而使得这些隐向量的内积尽可能地接近已知的矩阵元素。类似地，NMF采用了具有特定步长的随机梯度下降算法以确保隐向量的非负性。此外，GMF对上述这些传统的矩阵分解方法进行了优化，通过将内积替换为神经网络增强了模型的学习能力。然而，问题在于GMF并没有整合任何有价值的辅助信息。

图2绘制了Funk MF，NMF，GMF以及SGMF在二十组随机创建的训练集和测试集上的RMSE性能和AUC性能。统计发现，SGMF的平均RMSE值为1.40，这远低于Funk MF的平均RMSE值（2.26）、NMF的平均RMSE值（1.72）以及GMF的平均RMSE值（1.56）。该实验结果意味着SGMF方法在AS跳数矩阵补全方面的效果更好，即使是与GMF相比，也能将矩阵补全的性能提升10.3%。此外，在缺失AS链路预测方面，AUC值越高说明分类器区分正类和负类的能力越强。观察发现，SGMF的平均AUC值（0.834）与Funk MF的平均AUC值（0.580）相比提高了43.8%，与NMF的平均AUC值（0.682）相比提高了22.3%，与GMF的平均AUC值（0.716）相比提高了16.5%。这些提升表明SGMF方法在缺失AS链路预测方面也展现出更强的分类性能。

图2 不同矩阵补全方法的性能对比

3.3 已知探针数量和分布的影响

考虑到为SGMF提供训练数据的探针（即已知探针）的数量和分布可能会影响到训练集的质量，进而影响SGMF的性能，本节对此进行了深入分析。

针对每组训练集和测试集，本节随机选择了𝕋中10%，20%，30%，50%以及70%的探针，并利用它们观察到的AS路径构建了一组新的训练集。需要说明的是，除了模型输入有所不同之外，SGMF模型的初始参数设置以及超参数设置均保持不变。图3(a)展示了SGMF模型在两组训练集和测试集上的性能评估结果。从图中可以看出，当用于训练的已知探针数量从10%增加到50%时，SGMF模型的RMSE性能以及AUC性能均得到了显著提升。后续随着更多随机选择的探针被用于构建训练集，SGMF模型性能一直保持相对稳定。这意味着如果未来研究人员只是随机部署更多的探针，可能会仅提供大量冗余的AS跳数距离信息，对于提升SGMF在跳数矩阵补全以及缺失链路预测方面的性能没有什么帮助。

为了进一步研究已知探针的地理分布对SGMF性能的影响，需要先将探针准确地映射到相应的地理位置。为此，本节从Routeviews网站中提取了Routeviews探针的城市级地理位置信息，并购买了IP2Location地理定位库对RIPE RIS探针进行定位。接着，针对每组训练集和测试集，本节依次选择了𝕋中位于非洲（Africa，简称AF）、亚太地区（Asia Pacific，简称AP）、欧洲（Europe，简称EU）、拉丁美洲（Latin America，简称LA）以及北美（North America，简称NA）的探针，并利用它们观察到的AS路径构建了一组新的训练集。图3(b)展示了已知探针的地理分布情况对SGMF模型性能的影响。从图中可以看出，如果用于提供训练数据的已知探针在地理上分布不平衡，将会严重影响SGMF的RMSE性能和AUC性能。以第一组训练集和测试集为例，位于欧洲的530个探针所观察到的AS跳数距离信息只能帮助训练得到一个AUC值为0.6420（RMSE值为1.6655）的SGMF模型，相比于使用位于所有区域的探针训练得到的SGMF模型，性能下降了17.34%（16.70%）。此外，如图3(a)所示，同等数量（530/|𝕋|⩾50%）且分布在不同地理区域的已知探针可以帮助实现更好的性能。结果表明，如果研究人员多部署一些地理上均匀分布的探针将会带来丰富的AS跳数距离信息，从而有助于进一步提升SGMF的性能。

图3 已知探针的数量和分布对SGMF性能的影响

3.4 缺失链路预测结果

借助训练得到的SGMF模型，本节可以估计任意两个AS之间的跳数距离，进而计算跳数距离的倒数以得到它们之间存在链路的可能性。通过将预测的跳数距离与给定的阈值T进行比较，可以获得缺失AS链路预测结果。

图4展示了在一组随机拆分的训练集和测试集的基础上，训练好的SGMF模型在不同阈值设定下的FPR以及TPR分布情况。需要说明的是，本节在选择阈值T时，需要在真实存在的AS链路中未能被成功预测的比例（1-TPR）与实际并不存在的链路中被错误预测的比例（FPR）之间进行一定的权衡。从某种程度上来讲，本节愿意错失一定比例的链路，以换取大幅度降低实际不存在的AS链路中被错误预测为存在的比例，从而节省大量非必要的探测资源。为此，本节选择阈值T为2.94以实现较低的FPR（12.94%）以及可接受的TPR（70.09%）。换句话而言，SGMF方法可以成功过滤掉AS链路测试集中87.06%（1- FPR）的不存在的链路，这将避免大量用于试图发现这些不存在的链路而发起的非必要的测量，节省资源开销。与此同时，SGMF还可以成功识别AS链路测试集中70.09%的AS链路，有助于带来显著的拓扑完整性改进。

接着，本节进行了交叉验证以评估SGMF模型的泛化能力。图5绘制了当阈值T为2.94时，SGMF在二十组随机拆分的训练集和测试集上的FPR以及TPR分布情况。结果表明，T为2.94的SGMF模型在多个测试集上能达到TPR均值为66.87%、FPR均值为14.65%的分类性能，这与上述在单个AS链路测试集上的性能表现类似。随后，本节利用训练好的SGMF模型来预测互联网域间拓扑中未知的部分（共5.17 × 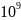个未知矩阵元素），发现其中存在9.28 × 条链路。该链路预测结果将有助于指导测量以获得高效的拓扑完整性提升。

图4 训练好的SGMF模型在不同阈值设定下的性能表现  

图5 SGMF在不同组训练集和测试集上的FPR以及TPR分布情况

3.5 使用不同的数据集进行验证

由于互联网是一个大规模、分布式的系统，并没有集中的控制机构，研究人员几乎不可能获得完整准确的互联网域间拓扑来验证上述SGMF模型得到的AS链路预测结果。在许多互联网规模的推断研究中（例如AS商业关系推断、互联网路由推断以及IP地址到地理位置的映射推断），缺乏基本事实是一个普遍存在的问题，而且未能被很好地解决。上述交叉验证将小部分BGP路由数据拆分出来作为基本事实以获取性能评估结果。由于训练集和测试集来自同一数据集，研究人员可能会质疑评估结果相比于实际情况存在一定的高估。为了使评估结果更加可靠，本节采用CAIDA公布的基于Ark测量基础设施采集的AS拓扑数据集（与训练集来自不同的数据源）进行进一步验证。

本节采集了CAIDA于2020年5月17日公布的AS链路数据集，该数据集包含了直接AS链路（在traceroute路径中具有两个相邻跃点）和间接AS链路（在traceroute路径中由一个或多个未映射或无响应的跃点分隔）。为了避免错误推断对拓扑构建产生影响，本节删除了该数据集中的间接AS链路，共得到了74,480条AS链路。接着移除其中在Routeviews以及RIPE RIS公布的BGP路由数据中出现过的AS链路，发现还剩下27,496条特有的AS链路。这些链路可以用来评估SGMF的缺失AS链路预测结果，观察发现其中大量的（17,665条）特有AS链路被SGMF成功地预测为存在。作为比较，本节还复现了现有最先进的缺失AS链路预测算法Toposcope^[1]并获得了相应的缺失链路预测结果，发现上述27,496条特有AS链路中仅有极少量的（366条）链路被成功地预测为存在。由此可以得出结论，本章提出的SGMF方法能够预测较多的缺失AS链路。

上述分析结果还可以用来评估SGMF的缺失AS链路预测结果在指导拓扑测量方面的性能表现。一方面，Ark测量基础设施所特有观察到的AS链路证明了大量的预测链路（17,665条）是真实存在的。虽然这只是通过小规模测量得到的一个下限，但表明未来有机会从SGMF预测存在的AS链路集合中观察到大量的缺失AS链路。另一方面，Ark测量基础设施特有观察到的AS链路中大部分（64.25%）链路都能被SGMF成功地预测为存在，这意味着未来能在SGMF预测结果的指导下发现全球缺失AS链路总量的64%左右。该实验结果与上述交叉验证得到的TPR均值（66.87%）较为接近，这也证明了之前的性能评估结果具有一定的可靠性。

参考文献

[1] Jin Z, Shi X, Yang Y, et al. Toposcope: Recover AS relationships from fragmentary observations[C/OL]//IMC ’20: Proceedings of the ACM Internet Measurement Conference. New York, NY, USA: ACM, 2020: 266–280.

[2] Faggiani A, Gregori E, Improta A, et al. A study on traceroute potentiality in revealing theInternet AS-level topology[C/OL]//2014 IFIP Networking Conference. Trondheim, Norway: IEEE, 2014: 1-9.

[3] Kumar A, Singh S S, Singh K, et al. Link prediction techniques, applications, and performance:A survey[J/OL]. Physica A: Statistical Mechanics and its Applications, 2020, 553: 124289.

[4] Yuliansyah H, Othman Z A, Bakar A A. Taxonomy of link prediction for social network analysis:A review[J/OL]. IEEE Access, 2020, 8: 183470-183487.

[5] Coşkun M, Koyutürk M. Node similarity-based graph convolution for link prediction in biological networks[J]. Bioinformatics, 2021, 37(23): 4501-4508.

[6] Li X, Chen H. Recommendation as link prediction in bipartite graphs: A graph kernel-based machine learning approach[J/OL]. Decision Support Systems, 2013, 54(2): 880-890.

[7] Eriksson B, Barford P, Sommers J, et al. Inferring unseen components of the Internet core[J/OL]. IEEE Journal on Selected Areas in Communications, 2011, 29(9): 1788-1798.

[8] Xue H J, Dai X Y, Zhang J, et al. Deep matrix factorization models for recommender systems[C/OL]//IJCAI’17: Proceedings of the 26th International Joint Conference on Artificial Intelligence. AAAI Press, 2017: 3203–3209.https://doi.org/10.24963/ijcai.2017/447.

[9] He X, Liao L, Zhang H, et al. Neural collaborative filtering[C/OL]//WWW ’17: CompanionProceedings of the Web Conference 2017. Republic and Canton of Geneva, CHE: ACM, 2017: 173–182.

[10] Ibrahim N M A, Chen L, Wang Y, et al. Deepeye: Link prediction in dynamic networks basedon non-negative matrix factorization[J/OL]. Big Data Min. Anal., 2018, 1(1): 19-33.

[11] Xie K, Chen Y, Wang X, et al. Accurate and fast recovery of network monitoring data: A GPU accelerated matrix completion[J/OL]. IEEE/ACM Transactions on Networking, 2020, 28(3): 958-971.

[12] Wang F, Gao L. On inferring and characterizing Internet routing policies[C/OL]//IMC ’03:Proceedings of the ACM Internet Measurement Conference. New York, NY, USA: ACM, 2003: 15–26.

[13] CAIDA. The CAIDA AS Relationships Dataset[EB/OL]. [2022-03-01].http://www.caida.org/data/active/as-relationships/.

[14] Zhou H, Zhang D, Xie K, et al. Data reconstruction in Internet traffic matrix[J]. China Communications, 2014, 11(7): 1-12.

[15] Shapira T, Shavitt Y. A deep learning approach for IP hijack detection based on ASN embedding[C/OL]//NetAI ’20: Proceedings of the Workshop on Network Meets AI & ML. New York, NY, USA: ACM, 2020: 35–41.

END

精彩推荐

BGP community——一类功能强大的BGP路由属性

面向大规模实时视频流的Overlay路由决策算法

IPv6移动通信网络用户设备往返时延的测量与分析