最近要给新生们出密码学的题,密码学白痴小肉鸡枯了,只能先学一波
简单概要
rsa是非对称加密,具体非对称加密是什么就不解释了,网上也有很多介绍,接下来我们直接进入加解密的过程
模逆运算
如果( a * b ) % c = 1,那么a和b互为对方模c的模逆元或叫数论倒数,也写成
1 2 3 4 5 6 7 8 9
证:给予两个整数a、b,必然存在整数x、y使得ax+by=gcd(a,b) 两边除gcd(a,b),右边成了1,左边a和b除了gcd(a,b)以后,新的a和b就互质 即证明ax+by=1 gcd(a,b)=1有整数解 想要证明ax+by=1 ab互质有整数解,那就是证明(a%b)*x1+b*y1=1有解 又辗转相除法可知,gcd(a,b)=gcd(b,a%b),即ab互质则b和a%b也会互质 让a=b,b=a%b,可得b*x1+(a%b)*y1=1 继续a=a%b,b=((a%b)%b),可得(a%b)*x2+((a%b)%b)*y2=1 ... 最后得到a=1,b=0,即1*xn+0*yn=1,显然成立,证毕
求逆元方法
1 2 3 4 5 6 7 8 9
def egcd (a,b) : if b==0 : return 1 ,0 ,a else : x,y,q = egcd(b,a%b) x,y = y,(x-(a//b)*y) return x,y,q def mod_inv (a,b) : return egcd(a,b)[0 ]%b
gmpy2库
1 2
import gmpy2print gmpy2.invert(47 ,30 )
欧几里得算法
就是辗转相除法
1 2
def gcd (a,b) : return a if not b else gcd(b,a%b)
扩展欧几里得算法
就是上面求逆元的那个迭代
1 2 3 4 5 6 7
def egcd (a,b) : if (b==0 ): return 1 ,0 ,a else : x1,y1,q = egcd(b,a%b) x,y = y1,(x1-(a//b)*y1) return x,y,q
例题
概念题
jarvisoj veryeasyRSA
题目给了pqe三个值,要求算d
1 2 3
p = 3487583947589437589237958723892346254777 q = 8767867843568934765983476584376578389 e = 65537
当然可以手工算,也可以直接扔去rsatool去算
jarvisoj Easy RSA
这题比起原来的题稍微难一点点,给了n,e和密文,要求算明文
1 2
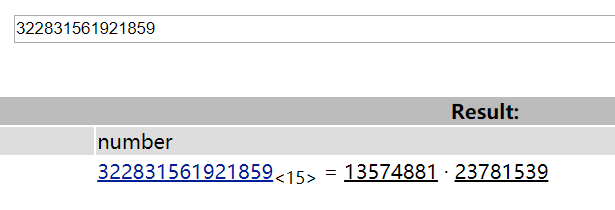
已知一段RSA加密的信息为:0xdc2eeeb2782c且已知加密所用的公钥: (N=322831561921859 e = 23)
先去factordb.com分解一下n,算出p和q
模数相关攻击
直接分解n
攻击条件
当n小于512位时,可以直接大数分解得到p和q
jarvisoj medium rsa
题目给了flag.enc和pubkey.pem文件,先用openssl命令提取信息
1
openssl rsa -pubin -in pubkey.pem -text -modulus
得到
1 2 3 4 5 6 7 8 9 10 11 12
Public-Key: (256 bit) Modulus: 00:c2:63:6a:e5:c3:d8:e4:3f:fb:97:ab:09:02:8f: 1a:ac:6c:0b:f6:cd:3d:70:eb:ca:28:1b:ff:e9:7f: be:30:dd Exponent: 65537 (0x10001) Modulus=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD writing RSA key -----BEGIN PUBLIC KEY----- MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr yigb/+l/vjDdAgMBAAE= -----END PUBLIC KEY-----
可以知道n是0xC2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD
1 2
p=275127860351348928173285174381581152299 q=319576316814478949870590164193048041239
然后解密
1 2 3 4 5 6 7 8 9 10 11 12 13 14
import libnumfrom Crypto.Util.number import long_to_bytesp=275127860351348928173285174381581152299 q=319576316814478949870590164193048041239 n = 87924348264132406875276140514499937145050893665602592992418171647042491658461 e = 65537 d = libnum.invmod(e,(p-1 )*(q-1 )) with open('flag.enc' ,'r' ) as f: c = f.read().encode('hex' ) c = int(c,16 ) m = pow(c,d,n) print long_to_bytes(m)
p和q选取不当使n可分解
攻击条件
如果p和q选择不当,使得n可以快速分解|p-q|较大 |p-q|较小 p-1光滑 p+1光滑
SECCON2017 very smooth
拿到一个pcap文件,分离一下
然后就会有三个证书文件,15A5.crt 8F4.crt FC6.crt
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128
openssl x509 -inform der -in FC6.crt -pubkey -text -modulus -noout -----BEGIN PUBLIC KEY----- MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDVRqqCXPYd6Xdl9GT7/kiJrYvy 8lohddAsi28qwMXCe2cDWuwZKzdB3R9NEnUxsHqwEuuGJBwJwIFJnmnvWurHjcYj DUddp+4X8C9jtvCaLTgd+baSjo2eB0f+uiSL/9/4nN+vR3FliRm2mByeFCjppTQl yioxCqbXYIMxGO4NcQIDAQAB -----END PUBLIC KEY----- Certificate: Data: Version: 1 (0x0) Serial Number: a1:8b:63:0c:7b:30:99:df Signature Algorithm: sha256WithRSAEncryption Issuer: C = JP, ST = Kawasaki, O = SRL Validity Not Before: Oct 8 02:47:17 2017 GMT Not After : Oct 8 02:47:17 2018 GMT Subject: C = JP, ST = Kawasaki, O = SRL Subject Public Key Info: Public Key Algorithm: rsaEncryption Public-Key: (1024 bit) Modulus: 00:d5:46:aa:82:5c:f6:1d:e9:77:65:f4:64:fb:fe: 48:89:ad:8b:f2:f2:5a:21:75:d0:2c:8b:6f:2a:c0: c5:c2:7b:67:03:5a:ec:19:2b:37:41:dd:1f:4d:12: 75:31:b0:7a:b0:12:eb:86:24:1c:09:c0:81:49:9e: 69:ef:5a:ea:c7:8d:c6:23:0d:47:5d:a7:ee:17:f0: 2f:63:b6:f0:9a:2d:38:1d:f9:b6:92:8e:8d:9e:07: 47:fe:ba:24:8b:ff:df:f8:9c:df:af:47:71:65:89: 19:b6:98:1c:9e:14:28:e9:a5:34:25:ca:2a:31:0a: a6:d7:60:83:31:18:ee:0d:71 Exponent: 65537 (0x10001) Signature Algorithm: sha256WithRSAEncryption 78:92:11:fb:6c:e1:7a:f7:2a:33:b8:8b:08:a7:f7:5b:de:cf: 62:0b:a0:ed:be:d0:69:88:38:93:94:9d:05:41:73:bd:7e:b3: 32:ec:8e:10:bc:3a:62:b0:56:c7:c1:3f:60:66:a7:be:b9:46: f7:46:22:6a:f3:5a:25:d5:66:94:57:0e:fc:b5:16:33:05:1c: 6f:f5:85:74:57:a4:a0:c6:ce:4f:fd:64:53:94:a9:83:b8:96: bf:5b:a7:ee:8b:1e:48:a7:d2:43:06:0e:4f:5a:86:62:69:05: e2:c0:bd:4e:89:c9:af:04:4a:77:a2:34:86:6a:b8:d2:3b:32: b7:39 Modulus=D546AA825CF61DE97765F464FBFE4889AD8BF2F25A2175D02C8B6F2AC0C5C27B67035AEC192B3741DD1F4D127531B07AB012EB86241C09C081499E69EF5AEAC78DC6230D475DA7EE17F02F63B6F09A2D381DF9B6928E8D9E0747FEBA248BFFDFF89CDFAF4771658919B6981C9E1428E9A53425CA2A310AA6D760833118EE0D71 openssl x509 -inform der -in 15A5.crt -pubkey -text -modulus -noout -----BEGIN PUBLIC KEY----- MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDVRqqCXPYd6Xdl9GT7/kiJrYvy 8lohddAsi28qwMXCe2cDWuwZKzdB3R9NEnUxsHqwEuuGJBwJwIFJnmnvWurHjcYj DUddp+4X8C9jtvCaLTgd+baSjo2eB0f+uiSL/9/4nN+vR3FliRm2mByeFCjppTQl yioxCqbXYIMxGO4NcQIDAQAB -----END PUBLIC KEY----- Certificate: Data: Version: 1 (0x0) Serial Number: a1:8b:63:0c:7b:30:99:df Signature Algorithm: sha256WithRSAEncryption Issuer: C = JP, ST = Kawasaki, O = SRL Validity Not Before: Oct 8 02:47:17 2017 GMT Not After : Oct 8 02:47:17 2018 GMT Subject: C = JP, ST = Kawasaki, O = SRL Subject Public Key Info: Public Key Algorithm: rsaEncryption Public-Key: (1024 bit) Modulus: 00:d5:46:aa:82:5c:f6:1d:e9:77:65:f4:64:fb:fe: 48:89:ad:8b:f2:f2:5a:21:75:d0:2c:8b:6f:2a:c0: c5:c2:7b:67:03:5a:ec:19:2b:37:41:dd:1f:4d:12: 75:31:b0:7a:b0:12:eb:86:24:1c:09:c0:81:49:9e: 69:ef:5a:ea:c7:8d:c6:23:0d:47:5d:a7:ee:17:f0: 2f:63:b6:f0:9a:2d:38:1d:f9:b6:92:8e:8d:9e:07: 47:fe:ba:24:8b:ff:df:f8:9c:df:af:47:71:65:89: 19:b6:98:1c:9e:14:28:e9:a5:34:25:ca:2a:31:0a: a6:d7:60:83:31:18:ee:0d:71 Exponent: 65537 (0x10001) Signature Algorithm: sha256WithRSAEncryption 78:92:11:fb:6c:e1:7a:f7:2a:33:b8:8b:08:a7:f7:5b:de:cf: 62:0b:a0:ed:be:d0:69:88:38:93:94:9d:05:41:73:bd:7e:b3: 32:ec:8e:10:bc:3a:62:b0:56:c7:c1:3f:60:66:a7:be:b9:46: f7:46:22:6a:f3:5a:25:d5:66:94:57:0e:fc:b5:16:33:05:1c: 6f:f5:85:74:57:a4:a0:c6:ce:4f:fd:64:53:94:a9:83:b8:96: bf:5b:a7:ee:8b:1e:48:a7:d2:43:06:0e:4f:5a:86:62:69:05: e2:c0:bd:4e:89:c9:af:04:4a:77:a2:34:86:6a:b8:d2:3b:32: b7:39 Modulus=D546AA825CF61DE97765F464FBFE4889AD8BF2F25A2175D02C8B6F2AC0C5C27B67035AEC192B3741DD1F4D127531B07AB012EB86241C09C081499E69EF5AEAC78DC6230D475DA7EE17F02F63B6F09A2D381DF9B6928E8D9E0747FEBA248BFFDFF89CDFAF4771658919B6981C9E1428E9A53425CA2A310AA6D760833118EE0D71 openssl x509 -inform der -in 8F4.crt -pubkey -text -modulus -noout -----BEGIN PUBLIC KEY----- MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDVRqqCXPYd6Xdl9GT7/kiJrYvy 8lohddAsi28qwMXCe2cDWuwZKzdB3R9NEnUxsHqwEuuGJBwJwIFJnmnvWurHjcYj DUddp+4X8C9jtvCaLTgd+baSjo2eB0f+uiSL/9/4nN+vR3FliRm2mByeFCjppTQl yioxCqbXYIMxGO4NcQIDAQAB -----END PUBLIC KEY----- Certificate: Data: Version: 1 (0x0) Serial Number: a1:8b:63:0c:7b:30:99:df Signature Algorithm: sha256WithRSAEncryption Issuer: C = JP, ST = Kawasaki, O = SRL Validity Not Before: Oct 8 02:47:17 2017 GMT Not After : Oct 8 02:47:17 2018 GMT Subject: C = JP, ST = Kawasaki, O = SRL Subject Public Key Info: Public Key Algorithm: rsaEncryption Public-Key: (1024 bit) Modulus: 00:d5:46:aa:82:5c:f6:1d:e9:77:65:f4:64:fb:fe: 48:89:ad:8b:f2:f2:5a:21:75:d0:2c:8b:6f:2a:c0: c5:c2:7b:67:03:5a:ec:19:2b:37:41:dd:1f:4d:12: 75:31:b0:7a:b0:12:eb:86:24:1c:09:c0:81:49:9e: 69:ef:5a:ea:c7:8d:c6:23:0d:47:5d:a7:ee:17:f0: 2f:63:b6:f0:9a:2d:38:1d:f9:b6:92:8e:8d:9e:07: 47:fe:ba:24:8b:ff:df:f8:9c:df:af:47:71:65:89: 19:b6:98:1c:9e:14:28:e9:a5:34:25:ca:2a:31:0a: a6:d7:60:83:31:18:ee:0d:71 Exponent: 65537 (0x10001) Signature Algorithm: sha256WithRSAEncryption 78:92:11:fb:6c:e1:7a:f7:2a:33:b8:8b:08:a7:f7:5b:de:cf: 62:0b:a0:ed:be:d0:69:88:38:93:94:9d:05:41:73:bd:7e:b3: 32:ec:8e:10:bc:3a:62:b0:56:c7:c1:3f:60:66:a7:be:b9:46: f7:46:22:6a:f3:5a:25:d5:66:94:57:0e:fc:b5:16:33:05:1c: 6f:f5:85:74:57:a4:a0:c6:ce:4f:fd:64:53:94:a9:83:b8:96: bf:5b:a7:ee:8b:1e:48:a7:d2:43:06:0e:4f:5a:86:62:69:05: e2:c0:bd:4e:89:c9:af:04:4a:77:a2:34:86:6a:b8:d2:3b:32: b7:39 Modulus=D546AA825CF61DE97765F464FBFE4889AD8BF2F25A2175D02C8B6F2AC0C5C27B67035AEC192B3741DD1F4D127531B07AB012EB86241C09C081499E69EF5AEAC78DC6230D475DA7EE17F02F63B6F09A2D381DF9B6928E8D9E0747FEBA248BFFDFF89CDFAF4771658919B6981C9E1428E9A53425CA2A310AA6D760833118EE0D71
待续……
模不互素
攻击条件
存在两个或以上模数,且gcd(n1,n2)!=1
攻击原理
如果两个n不互素的话,可以直接对这两个数求最大公因数,然后获得p和q,进而求得私钥
SCTF RSA2
公钥指数相关攻击
小公钥指数攻击
攻击条件
e十分小
例子
假设用户使用的密钥为3,加密过程是
那么就有
1 2
m³ = c + k*n m = ³√¯(c+k*n)¯
大黑阔可以从小到大枚举k,直到开出整数
jarvisoj Extremely hard RSA
题目给了pubkey.pem和flag.enc,然后openssl读下pubkey信息有
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54
Public-Key: (4096 bit) Modulus: 00:b0:be:e5:e3:e9:e5:a7:e8:d0:0b:49:33:55:c6: 18:fc:8c:7d:7d:03:b8:2e:40:99:51:c1:82:f3:98: de:e3:10:45:80:e7:ba:70:d3:83:ae:53:11:47:56: 56:e8:a9:64:d3:80:cb:15:7f:48:c9:51:ad:fa:65: db:0b:12:2c:a4:0e:42:fa:70:91:89:b7:19:a4:f0: d7:46:e2:f6:06:9b:af:11:ce:bd:65:0f:14:b9:3c: 97:73:52:fd:13:b1:ee:a6:d6:e1:da:77:55:02:ab: ff:89:d3:a8:b3:61:5f:d0:db:49:b8:8a:97:6b:c2: 05:68:48:92:84:e1:81:f6:f1:1e:27:08:91:c8:ef: 80:01:7b:ad:23:8e:36:30:39:a4:58:47:0f:17:49: 10:1b:c2:99:49:d3:a4:f4:03:8d:46:39:38:85:15: 79:c7:52:5a:69:98:4f:15:b5:66:7f:34:20:9b:70: eb:26:11:36:94:7f:a1:23:e5:49:df:ff:00:60:18: 83:af:d9:36:fe:41:1e:00:6e:4e:93:d1:a0:0b:0f: ea:54:1b:bf:c8:c5:18:6c:b6:22:05:03:a9:4b:24: 13:11:0d:64:0c:77:ea:54:ba:32:20:fc:8f:4c:c6: ce:77:15:1e:29:b3:e0:65:78:c4:78:bd:1b:eb:e0: 45:89:ef:9a:19:7f:6f:80:6d:b8:b3:ec:d8:26:ca: d2:4f:53:24:cc:de:c6:e8:fe:ad:2c:21:50:06:86: 02:c8:dc:dc:59:40:2c:ca:c9:42:4b:79:00:48:cc: dd:93:27:06:80:95:ef:a0:10:b7:f1:96:c7:4b:a8: c3:7b:12:8f:9e:14:11:75:16:33:f7:8b:7b:9e:56: f7:1f:77:a1:b4:da:ad:3f:c5:4b:5e:7e:f9:35:d9: a7:2f:b1:76:75:97:65:52:2b:4b:bc:02:e3:14:d5: c0:6b:64:d5:05:4b:7b:09:6c:60:12:36:e6:cc:f4: 5b:5e:61:1c:80:5d:33:5d:ba:b0:c3:5d:22:6c:c2: 08:d8:ce:47:36:ba:39:a0:35:44:26:fa:e0:06:c7: fe:52:d5:26:7d:cf:b9:c3:88:4f:51:fd:df:df:4a: 97:94:bc:fe:0e:15:57:11:37:49:e6:c8:ef:42:1d: ba:26:3a:ff:68:73:9c:e0:0e:d8:0f:d0:02:2e:f9: 2d:34:88:f7:6d:eb:62:bd:ef:7b:ea:60:26:f2:2a: 1d:25:aa:2a:92:d1:24:41:4a:80:21:fe:0c:17:4b: 98:03:e6:bb:5f:ad:75:e1:86:a9:46:a1:72:80:77: 0f:12:43:f4:38:74:46:cc:ce:b2:22:2a:96:5c:c3: 0b:39:29 Exponent: 3 (0x3) Modulus=B0BEE5E3E9E5A7E8D00B493355C618FC8C7D7D03B82E409951C182F398DEE3104580E7BA70D383AE5311475656E8A964D380CB157F48C951ADFA65DB0B122CA40E42FA709189B719A4F0D746E2F6069BAF11CEBD650F14B93C977352FD13B1EEA6D6E1DA775502ABFF89D3A8B3615FD0DB49B88A976BC20568489284E181F6F11E270891C8EF80017BAD238E363039A458470F1749101BC29949D3A4F4038D463938851579C7525A69984F15B5667F34209B70EB261136947FA123E549DFFF00601883AFD936FE411E006E4E93D1A00B0FEA541BBFC8C5186CB6220503A94B2413110D640C77EA54BA3220FC8F4CC6CE77151E29B3E06578C478BD1BEBE04589EF9A197F6F806DB8B3ECD826CAD24F5324CCDEC6E8FEAD2C2150068602C8DCDC59402CCAC9424B790048CCDD9327068095EFA010B7F196C74BA8C37B128F9E1411751633F78B7B9E56F71F77A1B4DAAD3FC54B5E7EF935D9A72FB176759765522B4BBC02E314D5C06B64D5054B7B096C601236E6CCF45B5E611C805D335DBAB0C35D226CC208D8CE4736BA39A0354426FAE006C7FE52D5267DCFB9C3884F51FDDFDF4A9794BCFE0E1557113749E6C8EF421DBA263AFF68739CE00ED80FD0022EF92D3488F76DEB62BDEF7BEA6026F22A1D25AA2A92D124414A8021FE0C174B9803E6BB5FAD75E186A946A17280770F1243F4387446CCCEB2222A965CC30B3929 writing RSA key -----BEGIN PUBLIC KEY----- MIICIDANBgkqhkiG9w0BAQEFAAOCAg0AMIICCAKCAgEAsL7l4+nlp+jQC0kzVcYY /Ix9fQO4LkCZUcGC85je4xBFgOe6cNODrlMRR1ZW6Klk04DLFX9IyVGt+mXbCxIs pA5C+nCRibcZpPDXRuL2BpuvEc69ZQ8UuTyXc1L9E7Huptbh2ndVAqv/idOos2Ff 0NtJuIqXa8IFaEiShOGB9vEeJwiRyO+AAXutI442MDmkWEcPF0kQG8KZSdOk9AON Rjk4hRV5x1JaaZhPFbVmfzQgm3DrJhE2lH+hI+VJ3/8AYBiDr9k2/kEeAG5Ok9Gg Cw/qVBu/yMUYbLYiBQOpSyQTEQ1kDHfqVLoyIPyPTMbOdxUeKbPgZXjEeL0b6+BF ie+aGX9vgG24s+zYJsrST1MkzN7G6P6tLCFQBoYCyNzcWUAsyslCS3kASMzdkycG gJXvoBC38ZbHS6jDexKPnhQRdRYz94t7nlb3H3ehtNqtP8VLXn75NdmnL7F2dZdl UitLvALjFNXAa2TVBUt7CWxgEjbmzPRbXmEcgF0zXbqww10ibMII2M5HNro5oDVE JvrgBsf+UtUmfc+5w4hPUf3f30qXlLz+DhVXETdJ5sjvQh26Jjr/aHOc4A7YD9AC LvktNIj3betive976mAm8iodJaoqktEkQUqAIf4MF0uYA+a7X6114YapRqFygHcP EkP0OHRGzM6yIiqWXMMLOSkCAQM= -----END PUBLIC KEY-----
e很小,所以我们可以直接进行指数攻击
1 2 3 4 5 6 7 8 9 10 11 12 13
import gmpy2,libnumn=0xB0BEE5E3E9E5A7E8D00B493355C618FC8C7D7D03B82E409951C182F398DEE3104580E7BA70D383AE5311475656E8A964D380CB157F48C951ADFA65DB0B122CA40E42FA709189B719A4F0D746E2F6069BAF11CEBD650F14B93C977352FD13B1EEA6D6E1DA775502ABFF89D3A8B3615FD0DB49B88A976BC20568489284E181F6F11E270891C8EF80017BAD238E363039A458470F1749101BC29949D3A4F4038D463938851579C7525A69984F15B5667F34209B70EB261136947FA123E549DFFF00601883AFD936FE411E006E4E93D1A00B0FEA541BBFC8C5186CB6220503A94B2413110D640C77EA54BA3220FC8F4CC6CE77151E29B3E06578C478BD1BEBE04589EF9A197F6F806DB8B3ECD826CAD24F5324CCDEC6E8FEAD2C2150068602C8DCDC59402CCAC9424B790048CCDD9327068095EFA010B7F196C74BA8C37B128F9E1411751633F78B7B9E56F71F77A1B4DAAD3FC54B5E7EF935D9A72FB176759765522B4BBC02E314D5C06B64D5054B7B096C601236E6CCF45B5E611C805D335DBAB0C35D226CC208D8CE4736BA39A0354426FAE006C7FE52D5267DCFB9C3884F51FDDFDF4A9794BCFE0E1557113749E6C8EF421DBA263AFF68739CE00ED80FD0022EF92D3488F76DEB62BDEF7BEA6026F22A1D25AA2A92D124414A8021FE0C174B9803E6BB5FAD75E186A946A17280770F1243F4387446CCCEB2222A965CC30B3929 e=3 res=0 c=int(open('flag.enc' ,'rb' ).read().encode('hex' ),16 ) for k in range(118700000 , 118750000 ): a, b = gmpy2.iroot(c+n*k,e) if b==1 : res=a print k print res print libnum.n2s(res) break
他的k是118719488,减小范围,跑的快一点,最后拿到flag
1
Didn't you know RSA padding is really important? Now you see a non-padding message is so dangerous. And you should notice this in future.Fl4g: PCTF{Sm4ll_3xpon3nt_i5_W3ak}
rabin算法
攻击条件
e = 2
攻击原理
密文
解密过程
1 2 3 4 5 6 7 8 9 10
算mp和mq mp = √c mod p mq = √c mod q 由扩展欧几里得算出 yp*p + yq*q = 1 得到四个明文 a = (yp*p*mq + yq*q*mp) mod n b = n - a c = (yp*p*mq - yq*q*mp) mod n d = n - c
如果 p ≡ q ≡ 3 (mod 4),那么
jarvisoj hardRSA
openssl提信息
1 2 3 4 5 6 7 8 9 10 11 12
Public-Key: (256 bit) Modulus: 00:c2:63:6a:e5:c3:d8:e4:3f:fb:97:ab:09:02:8f: 1a:ac:6c:0b:f6:cd:3d:70:eb:ca:28:1b:ff:e9:7f: be:30:dd Exponent: 2 (0x2) Modulus=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD writing RSA key -----BEGIN PUBLIC KEY----- MDowDQYJKoZIhvcNAQEBBQADKQAwJgIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr yigb/+l/vjDdAgEC -----END PUBLIC KEY-----
分解n得到
1 2
p = 275127860351348928173285174381581152299 q = 319576316814478949870590164193048041239
利用rabin算法去写脚本
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
import gmpy2import stringfrom Crypto.PublicKey import RSAwith open('pubkey.pem' ,'r' ) as f: key = RSA.importKey(f) n = key.n e = key.e with open('flag.enc' ,'r' ) as f: c = f.read().encode('hex' ) c = string.atoi(c,base=16 ) print "start" p = 275127860351348928173285174381581152299 q = 319576316814478949870590164193048041239 inv_p = gmpy2.invert(p,q) inv_q = gmpy2.invert(q,p) mp = pow(c,(p+1 )/4 ,p) mq = pow(c,(q+1 )/4 ,q) a = (inv_p * p * mq + inv_q * q * mp) % n b = n - int(n) c = (inv_p * p * mq - inv_q * q * mp) % n d = n - int(c) for i in (a,b,c,d): s = '%x' % i if len(s) % 2 != 0 : s = '0' +s print s.decode('hex' )
最后拿到flag:PCTF{sp3ci4l_rsa}










评论