对称密码算法有时又叫传统密码算法、秘密密钥算法或单密钥算法。对称密码算法的加密密钥能够从解密密钥中推算出来,反过来也成立。在大多数对称算法中,加密解密密钥是相同的。它要求发送者和接收者在安全通信之前,商定一个密钥。对称算法的安全性依赖于密钥,泄漏密钥就意味着任何人都能对消息进行加密解密。只要通信需要保密,密钥就必须保密。
对称算法又可分为两类。一次只对明文中的单个位(有时对字节)运算的算法称为序列算法或序列密码。另一类算法是对明文的一组位进行运算,这些位组称为分组,相应的算法称为分组算法或分组密码。现代计算机密码算法的典型分组长度为64位――这个长度既考虑到分析破译密码的难度,又考虑到使用的方便性。后来,随着破译能力的发展,分组长度又提高到128位或更长。
对称密码常用的数学运算
对称密码当中有几种常用到的数学运算。这些运算的共同目的就是把被加密的明文数码尽可能深地打乱,从而加大破译的难度。
◆移位和循环移位
移位就是将一段数码按照规定的位数整体性地左移或右移。循环右移就是当右移时,把数码的最后的位移到数码的最前头,循环左移正相反。例如,对十进制数码12345678循环右移1位(十进制位)的结果为81234567,而循环左移1位的结果则为23456781。
◆置换
就是将数码中的某一位的值根据置换表的规定,用另一位代替。它不像移位操作那样整齐有序,看上去杂乱无章。这正是加密所需,被经常应用。
◆扩展
就是将一段数码扩展成比原来位数更长的数码。扩展方法有多种,例如,可以用置换的方法,以扩展置换表来规定扩展后的数码每一位的替代值。
◆压缩
就是将一段数码压缩成比原来位数更短的数码。压缩方法有多种,例如,也可以用置换的方法,以表来规定压缩后的数码每一位的替代值。
◆异或
这是一种二进制布尔代数运算。异或的数学符号为⊕ ,它的运算法则如下:
1 |
1⊕1 = 0 |
也可以简单地理解为,参与异或运算的两数位如相等,则结果为0,不等则为1。
◆迭代
迭代就是多次重复相同的运算,这在密码算法中经常使用,以使得形成的密文更加难以破解。
DES
DES算法为密码体制中的对称密码体制。需要加密的明文按64位进行分组,加密密钥是根据用户输入的秘钥生成的,密钥长64位,但密钥事实上是56位参与DES运算(第8、16、24、32、40、48、56、64位是校验位, 使得每个密钥都有奇数个1,在计算密钥时要忽略这8位),分组后的明文组和56位的密钥按位替代或交换的方法形成密文组的加密方法
DES算法加密流程描述 :
(1)输入64位明文数据,并进行初始置换IP;
(2)在初始置换IP后,明文数据再被分为左右两部分,每部分32位,以L0,R0表示;
(3)在秘钥的控制下,经过16轮运算(f);
(4)16轮后,左、右两部分交换,并连接再一起,再进行逆置换;
(5)输出64位密文。
python实现
1 |
# -- coding: utf-8 --- |
3DES
由于DES密码长度容易被暴力破解,所以3DES算法通过对DES算法进行改进,增加DES的密钥长度来避免类似的攻击,针对每个数据块进行三次DES加密;因此,3DES加密算法并非什么新的加密算法,是DES的一个更安全的变形,它以DES为基本模块,通过组合分组方法设计出分组加密算法。。
加/解密过程
该算法的加解密过程分别是对明文/密文数据进行三次DES加密或解密,得到相应的密文或明文。
假设EK()和DK()分别表示DES的加密和解密函数,P表示明文,C表示密文,那么加解密的公式如下:
加密:C = EK3( DK2( EK1(P)) ),即对明文数据进行,加密 –> 解密 –> 加密的过程,最后得到密文数据;
解密:P = DK1( EK2( DK3(C)) ),即对密文数据进行,解密 –> 加密 –> 解密的过程,最后得到明文数据;
其中:K1表示3DES中第一个8字节密钥,K2表示第二个8字节密钥,K3表示第三个8字节密钥,K1、K2、K3决定了算法的安全性,若三个密钥互不相同,本质上就相当于用一个长为168位的密钥进行加密。多年来,它在对付强力攻击时是比较安全的。若数据对安全性要求不那么高,K1可以等于K3。在这种情况下,密钥的有效长度为112位,即K1对应KL(左8字节),K2对应KR(右8字节),K3对应KL(左8字节)。
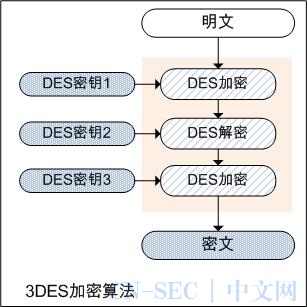
当三重密钥均相同时,前两步相互抵消,相当于仅实现了一次加密,因此可实现对普通DES加密算法的兼容。
AES
AES为分组密码,分组密码也就是把明文分成一组一组的,每组长度相等,每次加密一组数据,直到加密完整个明文。在AES标准规范中,分组长度只能是128位,也就是说,每个分组为16个字节(每个字节8位)。密钥的长度可以使用128位、192位或256位。密钥的长度不同,推荐加密轮数也不同,如下表所示:
| AES | 密钥长度(32位比特字) | 分组长度(32位比特字) | 加密轮数 |
|---|---|---|---|
| AES-128 | 4 | 4 | 10 |
| AES-192 | 6 | 4 | 12 |
| AES-256 | 8 | 4 | 14 |
轮数在下面介绍,这里实现的是AES-128,也就是密钥的长度为128位,加密轮数为10轮。
上面说到,AES的加密公式为C = E(K,P),在加密函数E中,会执行一个轮函数,并且执行10次这个轮函数,这个轮函数的前9次执行的操作是一样的,只有第10次有所不同。也就是说,一个明文分组会被加密10轮。AES的核心就是实现一轮中的所有操作。
AES的处理单位是字节,128位的输入明文分组P和输入密钥K都被分成16个字节,分别记为P = P0 P1 … P15 和 K = K0 K1 … K15。如,明文分组为P = abcdefghijklmnop,其中的字符a对应P0,p对应P15。一般地,明文分组用字节为单位的正方形矩阵描述,称为状态矩阵。在算法的每一轮中,状态矩阵的内容不断发生变化,最后的结果作为密文输出。该矩阵中字节的排列顺序为从上到下、从左至右依次排列,如下图所示: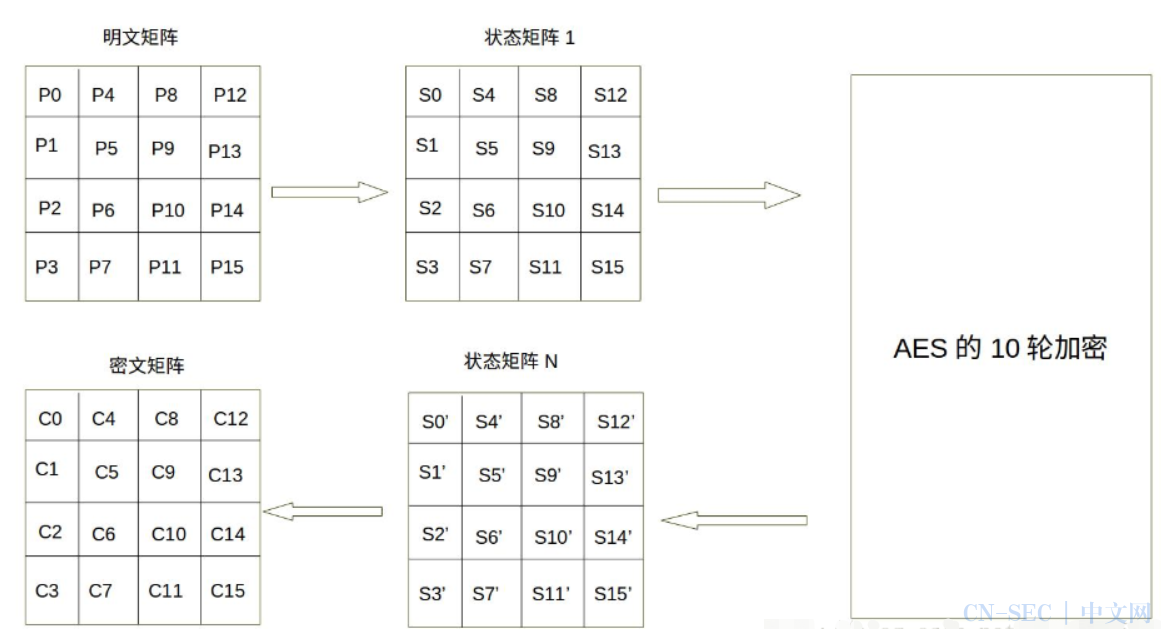
现在假设明文分组P为”abcdefghijklmnop”,则对应上面生成的状态矩阵图如下:
上图中,0x61为字符a的十六进制表示。可以看到,明文经过AES加密后,已经面目全非。
类似地,128位密钥也是用字节为单位的矩阵表示,矩阵的每一列被称为1个32位比特字。通过密钥编排函数该密钥矩阵被扩展成一个44个字组成的序列W[0],W[1], … ,W[43],该序列的前4个元素W[0],W[1],W[2],W[3]是原始密钥,用于加密运算中的初始密钥加(下面介绍);后面40个字分为10组,每组4个字(128比特)分别用于10轮加密运算中的轮密钥加,如下图所示:
上图中,设K = “abcdefghijklmnop”,则K0 = a, K15 = p, W[0] = K0 K1 K2 K3 = “abcd”。
AES的整体结构如下图所示,其中的W[0,3]是指W[0]、W[1]、W[2]和W[3]串联组成的128位密钥。加密的第1轮到第9轮的轮函数一样,包括4个操作:字节代换、行位移、列混合和轮密钥加。最后一轮迭代不执行列混合。另外,在第一轮迭代之前,先将明文和原始密钥进行一次异或加密操作。
上图也展示了AES解密过程,解密过程仍为10轮,每一轮的操作是加密操作的逆操作。由于AES的4个轮操作都是可逆的,因此,解密操作的一轮就是顺序执行逆行移位、逆字节代换、轮密钥加和逆列混合。同加密操作类似,最后一轮不执行逆列混合,在第1轮解密之前,要执行1次密钥加操作
分组密码模式
DES 和 AES 都属于分组密码,他们只能加密固定长度的明文。
分组加密会将明文消息划分为固定大小的块,每块明文分别在密钥控制下加密为密文。当然并不是每个消息都是相应块大小的整数倍,所以我们可能需要进行填充。
ECB
ECB 模式全称为电子密码本模式(Electronic codebook),在ECB模式中,将明文分组加密之后的结果将直接成为密文分组。
加密:
解密:
攻击方式
直接找几组不同的密文,然后截取再拼接进行重放攻击
CBC
CBC 全称为密码分组链接(Cipher-block chaining) 模式。在CBC模式中,首先将明文分组与前一个密文分组进行XOR运算,然后再进行加密。
加密:
解密:
CBC字节翻转攻击
Padding oracle attack
填充提示攻击是一种利用分组密码中的填充部分来进行攻击的方法,在分组密码中,当明文长度不为分组长度的整数倍时,需要在最后一个分组中填充一些数据使其凑满一个分组长度。
https://www.freebuf.com/articles/web/15504.html
CFB
CFB 全称为密文反馈模式(Cipher feedback)。明文分组和密文分组之间并没有经过加密这一步骤,只有一个XOR。
重放攻击
OFB
FB 全称为输出反馈模式(Output feedback),其反馈内容是分组加密后的内容而不是密文
加密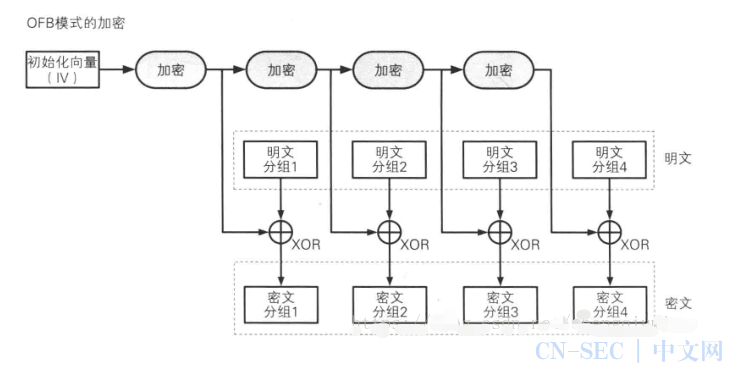
解密
CTR
CTR 模式全称是CounTeR模式(计数器模式),CTR模式是一种通过将逐次累积的计数器进行加密来生成密钥流的流密码。
加密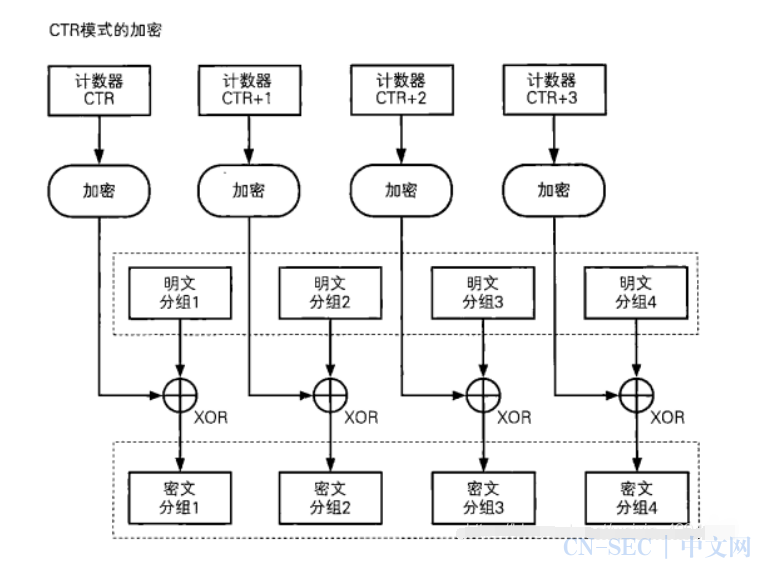
解密
参考文章
DES加密算法原理:whttps://www.jianshu.com/p/c44a8a1b7c38
DES加密算法分析:http://ronpa.top/2018/08/20/DES%E5%8A%A0%E5%AF%86%E7%AE%97%E6%B3%95%E5%88%86%E6%9E%90/
AES 加密算法的原理详解:https://blog.csdn.net/gulang03/article/details/81175854
ctfwiki:https://ctf-wiki.org/crypto/blockcipher/mode/introduction/
FROM :blog.cfyqy.com | Author:cfyqy
- 左青龙
- 微信扫一扫
-

- 右白虎
- 微信扫一扫
-









评论