0x00 前言
应该是4月左右的一个比赛,里面有一道crypto题,可以学到rsa几个特殊性质,对做ctf的crypto手应该会比较有帮助。
原题:
import osfrom Crypto.Util.number import *from secret import flagbits = 512def pad(msg, length):pad_length = length - len(msg) - 1pad_data = os.urandom(pad_length)return msg + b'x00' + pad_datadef unpad(msg):return msg.split(b"x00")[0]def challenge1(m):p, q = [getPrime(bits) for i in range(2)]if p <= q:p, q = q, pe = 0x10001n = p * qc = pow(m, e, n)leak = (n + p) % (q-1)print('-------- challenge 1 --------')print(f'{e = }')print(f'{c = }')print(f'{n = }')print(f'{leak = }')def challenge2(m):p, q = [getPrime(bits) for i in range(2)]e = 0x10001n = p * qd = inverse(e, (p-1)*(q-1))c = pow(m, e, n)leak = d + p + qprint('-------- challenge 2 --------')print(f'{e = }')print(f'{c = }')print(f'{n = }')print(f'{leak = }')def challenge3(m):p, q = [getPrime(bits) for i in range(2)]e = 0x10001n = p * qc = pow(m, e, n)leak = (pow(p, q, n) + pow(q, p, n)) % nprint('-------- challenge 3 --------')print(f'{e = }')print(f'{c = }')print(f'{n = }')print(f'{leak = }')assert len(flag) == 42ms = []for i in range(0, 42, 14):ms.append(bytes_to_long(pad(flag[i:i+14], bits//4-1)))m1, m2, m3 = mschallenge1(m1)challenge2(m2)challenge3(m3)"""-------- challenge 1 --------e = 65537c = 112742443814287255411540092433156061065388404049949520959549377871297566383025041892192679147481155020865118811016470498351633875090973546567374001852295013083192495299811476604405637385307524194793969533646755764136014187430115618114840780368311166911900457224593131166970676797547489278410997707815915932756n = 121127425328043404860413278637978444801342472819958112597540188142689720655042880213001676368390521140660355813910726809125567752172921410143437643574528335234973793653775043030021036875866776532570781661875022102733555943967261003246543180935987772711036868216508554536086688819118597075508026787867088355603leak = 216638862637129382765636503118049146067015523924032194492700294200289728064297722088882791754351329407138196573832392846467607399504585045028165699421278-------- challenge 2 --------e = 65537c = 7964477910021153997178145480752641882728907630831216554750778499596527781702830885213467912351097301767341858663701574005489585561370961723264247818377063081744522471774208105250855114831033452448184392499682147532404562876275189577321587660597603848038824026981539659156304028998137796242331160312370913038n = 140571013522095816880929287025269553867630639381779595547026503691829940612178900269986625350464874598461222087427155791855120339533208468121389480964471710028253589422629569889402475311387750348466199387760629889238062977271925350490110043385800605640905324122017637306715108727700910035925728362455954862209leak = 58442382248753295429370894053397615609981110383986887405127350139482893508400422595729520437678203735054593866306478994471465948872565590901376309380029015549809468112086393107585011072503638322671608471684607214064187044372418770555236721845694224676090744181562673509234801011420696349507624867568099759003-------- challenge 3 --------e = 65537c = 54161995127842474543974770981473422085334044100057089719350274921419091368361244533281599379235907845996678762379778310924192757650322930707785543132446159092950451255660204858292974657119337026589911330412367633761103944916751660957776230135927005700707688661350641600954072696774954805514477330339449799540n = 88207747624007183083381863279444163105330473097729276113333026679597864128605555600000789783468271680476780366740448641311570797876037993255307716167149079618302706650018518487351604778857406170722209469765782625409279109832638886179654096975665134276856272488090272822541461702907181545730309689190333058151leak = 19596671928335648228117128090384865424885102632642665068992144783391306491716530155291726644158221224616817878768426330717188403310818678195631582453246848"""
0x01 赛题分析
这道题很好理解题目意思,flag的长度42,等分三部分,每部分长度14。然后分别对应challenge1,challenge2,challenge3三种加密方式。关键在于这三种rsa加密的特殊提示leak的利用,下面对三个challenge分开解密。
0x02 challgen1
challenge1:leak = (n + p) % (q-1)
根据题目条件,当p<=q时,交换p,q,所以p>=q。
(n + p) % (q-1) = (p*q + p) mod (q-1)
=p*(q + 1) mod (q - 1)
∵q+1 mod q-1 = (q + 1)-(q - 1) =2
∴上述式子 = 2*p mod (q - 1)
又∵p>=q
∴p>q-1
∴2*p mod (q - 1) = 2*p - k*(q - 1),k为1-4之间(因为p,q都是512位的素数,最大素数和最小素数差距在2倍之间,所以2p和q差距应该在1-4倍之间)
得到两个方程组:
① n=p*q
② leak=2*p - k*(q - 1)
通过sagemath解方程:
#sage k需要改成1-4
e = 65537
c = 112742443814287255411540092433156061065388404049949520959549377871297566383025041892192679147481155020865118811016470498351633875090973546567374001852295013083192495299811476604405637385307524194793969533646755764136014187430115618114840780368311166911900457224593131166970676797547489278410997707815915932756
n = 121127425328043404860413278637978444801342472819958112597540188142689720655042880213001676368390521140660355813910726809125567752172921410143437643574528335234973793653775043030021036875866776532570781661875022102733555943967261003246543180935987772711036868216508554536086688819118597075508026787867088355603
leak = 216638862637129382765636503118049146067015523924032194492700294200289728064297722088882791754351329407138196573832392846467607399504585045028165699421278
var('p q')
solve([2*p-k*(q-1)-leak, p*q-n],p,q)
最后尝试出k为2时,能解出正确的p,q
有了p,q就能按照一般rsa的解密过程,还原出明文,根据题目flag1取前14位
0x03 challgen2
Challenge2:leak = d + p + q
根据题目可得d = leak -(p+q)
Rsa的明文m=c^d % n
把d代入进去化简:
m = c^(leak -(p+q)) mod n
① c^(leak -(p+q))≡ c^leak * c^-(p+q) mod n
根据欧拉定理推论:
c^φ(n) ≡ 1 mod n
1 ≡ c^((p-1)(q-1))mod n
1 ≡ c^(p*q + 1 - (p+q)) mod n
1 ≡ c^(n+1) * c^-(p+q) mod n
② c^-(n+1) ≡ c^-(p+q) mod n
两个式子联合得:
明文m = c^leak * c^-(n+1) mod n
m = c^(leak - n -1) mod n
python程序求m,根据题目flag2取前14位
0x04 challgen3
Challenge3:leak = (pow(p, q, n) + pow(q, p, n)) % n
leak = ( p^q mod n + q^p mod n ) mod n
leak =(p^q + q^p )mod n
根据费马小定理:
p^φ(q) ≡ 1 mod q
P^(q - 1)*p≡ 1 *p mod q
p^q ≡ p mod q
p^q + q^p ≡ p + q^p mod q
① p^q + q^p ≡ p + 0 mod q
同理可得
② p^q + q^p ≡ q mod p
令a = p^q + q^p
则得到
① a ≡ p mod q
② a ≡ q mod p
可写为
① a = k1*q + p
a - p = k1*q
② a = k2*p + q
a - q = k2*p
两式相乘得
(a-p) * (a-q) = k1*k2*p*q
两边同时mod n得
a^2 -a*(p+q) + p*q ≡ k1*k2*p*q mod n
a^2 -a*(p+q) + 0 ≡ 0mod n
a^2 ≡ a*(p+q) mod n
如果a 和 n互质,则可以约去两边的一个a,使得同余关系变为
a ≡ p+q mod n
也就是(p^q + q^p) mod n = p+q
leak = p + q
证明a 和 n互质(可以跳过不看):
n是两个素数p,q的乘积,所以如果a和n有公因数,公因数必定为p或者为q,
a= p^q + q^p,分别让a mod p,a mod q ,看是否能整除,得
a mod p = p^q + q^p mod p = q^p + 0 mod p
=q*q^ (p-1) mod p
费马小定理q^(p-1) ≡ 1 mod p
∴① a mod p =q *1 mod p
同理② a mod q = p mod q
由此可得,当p≠q时,a不能和p或者q整除
说明当p≠q时,a和n互质
前面推断出了leak = p + q,就已经是经典类型的问题了,下面给出构造方程组的过程
leak^2 = (p+q)^2
leak^2 = p^2 + q^2 + 2*p*q
leak^2 - 4*p*q = p^2 + q^2 - 2*p*q
leak^2 - 4*n = (p-q)^2
(leak^2 - 4*n)^-2 = p - q
这下得出了p-q的值,之前有p+q的值,两个式子相加或者相减就能算出p和q
① (leak^2 - 4*n)^-2 + leak = 2*p
② leak - (leak^2 - 4*n)^-2 = 2*q
得出p,q后就是正常的rsa解密了
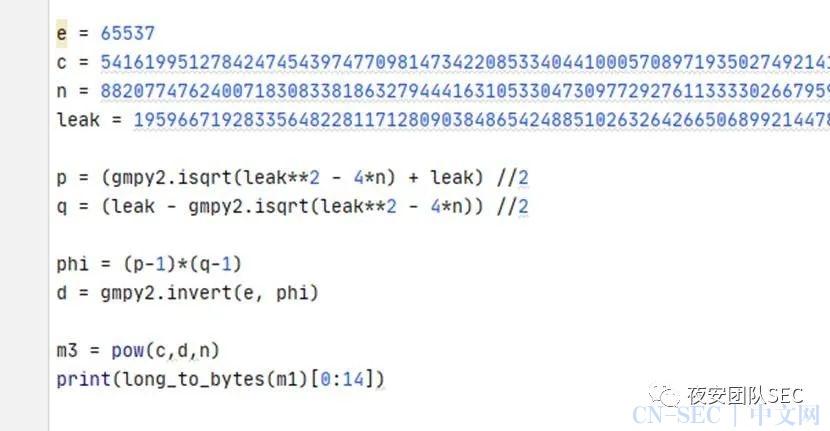
当然知道了leak= p+q,也可以不用求出p和q具体的数值,我们只需要计算n的欧拉函数phi就可以进行解密
Φ(n) = (p-1)*(q-1)
=p*q +1 - (p+q)
=n + 1 - leak
0x05 总结
这到题目还蛮有意思的,喜欢ctf加解密的师傅可以玩玩这道题。
原文始发于微信公众号(夜安团队SEC):CTF-密码学-math_exam解题分析详解---2023数字中国创新大赛网络数据安全赛道数据安全产业人才能力挑战赛
- 左青龙
- 微信扫一扫
-

- 右白虎
- 微信扫一扫
-











评论