NP问题及证明

一、几个概念

• P: can be solved in polynomial time

• NP: If the answer is YES + this fact that can be checked in polynomial time

• co-NP: If the answer is NO + this fact that can be checked in polynomial time

• NP-hard: no one in their right mind should believe a np-hard problem can be solved in polynomial time.

• Π is NP-hard ⇐⇒ If Π can be solved in polynomial time, then P=NP

• NP-complete:( the hardest problems in NP) it is both NP-hard and an element of NP. 

• 

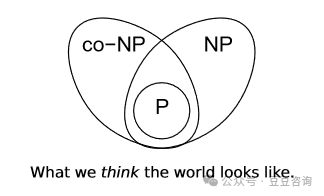
二、P、NP、NP-hard、NP-complete、co-NP总结

NP-Hard问题要比 NPC问题的范围广，

P问题就是指该问题能在多项式复杂度内解决。

NP问题就是指该问题能在多项式复杂度内被验证。

复杂度一般用大写字母O表示，多项式复杂度记为O(n(^k))。

NP-hard问题就是比NP问题更困难解决的问题，通常NP问题都可以说是NP-hard问题，但是不是所有的NP-hard问题都是NP问题（有些NP-hard问题无法被验证）

NP-complete（NPC问题）就是既是NP问题也是NP-hard问题。

三、证明

3.1 规约

To prove that problem A is NP-hard, reduce a known NP-hard problem to A.

reduction：如果能找到这样一个变化法则，对任意一个程序A的输入，都能按这个法则变换成程序B的输入，使两程序的输出相同，那么我们说，问题A可归约为问题B。

约化：问题A约化为问题B的含义就是，可以用问题B的解法解决A。例如我们有问题A：求解一元一次方程bx+c=0，问题B：求解二元一次方程ax^2+bx+c=0。如果我们知道问题B的解法，那么一定可以知道问题A的解法，因为只要我们令a=0，问题B就和问题A等价，所以我们可以说“问题A可约化为问题B”。很显然当我们说“问题A可约化为问题B”，那么问题B的时间复杂度一定高于或者等于问题A的时间复杂度。其次约化还具有一个重要性质：约化具有传递性。也就是说如果问题A可约化为问题B，问题B可约化为问题C，那么问题A一定可约化为问题C。

3.2 NP问题

    很多问题很难找到多项式时间的解法(不一定存在)，但我们可以在多项式时间内判断一个解是否正确。如下图(图片来源于维基百科)的哈密顿回路问题，目前没有多项式时间的算法找到哈密顿回路，但我们很容易判断一个回路是否是哈密顿回路(看是不是所有顶点都在回路中，并且路径不重复)。

3.3 NPC问题

    我们知道一个问题约化后，时间复杂度可能增加了，问题的应用范围也可能增大了。那么通过不断的约化，我们能否找到一个超级NP问题，使得所有的NP问题都可以约化到它？答案是肯定的，这就是NPC问题。可以想象如果我们解决了NPC问题，那么所有的NP问题都将被解决，这种问题的存在真的让人惊叹。此外NPC问题事实上不只一个，它有很多个，这是一类问题。很显然NPC问题是可以相互约化的，也就是说如果我们想证明一个问题是NPC问题，只要证明这个问题是NP问题并且已知的一个NPC问题可以约化到它。那么第一个NPC问题是怎么来的？布尔逻辑的可满足性问题(SATISFIABLITY problem)，简称为SAT，这是历史上第一个被证明的NPC问题。有了第一个NPC问题，一大堆NPC问题就出现了。事实上上文说的哈密顿回路问题就是一个NPC问题。

3.4 P=NP ?

现在人们特别想知道P是否等于NP，也就是说是否所有的NP问题都可以在多项式时间内解决。目前P=NP即不能被证明也不能被推翻，事实上我们只要能在多项式时间内解决NPC问题，那么所有的NP问题都可以在多项式时间内解决，也就是P=NP，然而目前已知的NPC问题都没有找到多项式时间的解法。所以现在人们主流认为P不等于NP。

参考文献

https://blog.csdn.net/u013288190/article/details/123271528

https://zhuanlan.zhihu.com/p/535780250

https://blog.51cto.com/shijianfeng/5153340

原文始发于微信公众号（豆豆咨询）：NP问题及证明