ADFGX密码、云影密码和希尔密码学习

改密码在加密和解密时需要输入两个东西，一个密码表，一个密钥，密码表时5x5的polybius表格，里面的字符是a-z(i和j看作同一个)打乱顺序的，出去j刚好填满25个格子。其中的横纵坐标是由ADFGX表示的，如密码表为：

“xyzdefghijklmnopqrstuvwcba”,如下：

再将刚刚查表后的字符串根据密钥如下排列（假设密钥是linux, 刚刚查表后得到的是

FXDDXGDFFGFFGG）：

再根据密钥字符的ascii码大小对上表的列按从小到大排列

最后按列将密文去除，如上表取出为：

XDFFGFDFFDFGXX。

特点：

• 密文长度是明文的两倍，即密文是偶数

• 密文字符仅有ADFGX这几个字符

有1，2，4，8这四个数字，可以通过加法来用这四个数字表示0-9中的任何一个数字，列如0=28， 也就是0=2+8，同理7=124， 9=18。这样之后再用1-26来表示26个英文字母，就有了密文与明文之间的对应关系。引入0来作为间隔，以免出现混乱。所以云影密码又叫“01248密码”。

希尔密码是一种基于线性代数的多表替换密码。使用希尔密码需要对矩阵的有基本的了解。希尔密码也是一种分块加密算法（block cipher），它接受输入的明文，并生成一个密文块。希尔密码是由Lester S在1929年发明的。是第一个同时处理三个及以上符号或字母的多表密码。下面的公式用于加密和解密：

其中，Plain是加密前的明文矩阵，Cipher是加密后的密文矩阵，Key是密钥矩阵（要求是一个方阵），N是字符集的大小，Key^−1是密钥矩阵在模N空间上的逆矩阵。

• 首先，选择一个整数n （通常n = 2 、3等小整数，这决定了密钥矩阵的阶数）。

• 然后构造一个  的可逆矩阵作为密钥矩阵K 。例如，当n = 2时，密钥矩阵可能是，

  其中矩阵的元素a,b,c,d  

• 是满足ad - bc != 0(mod 26)的整数（在处理英文字母时，因为英文字母有 26 个，所以通常是模 26 运算）。这是因为只有可逆矩阵才能保证解密的可行性。

• 把明文按照每n个字符一组进行划分。如果明文长度不是n的整数倍，需要在末尾添加适当的字符（如字母 'x'）来凑齐。例如，对于明文 “HELLO”，当n = 2时，可分为 “HE” 和 “LL” 和 “O（补 x）x” 三组。

• 对每个明文字符，根据字母表顺序将其转换为数字。通常，A 对应 0，B 对应 1，C 对应 2，……，Z 对应 25。例如，对于明文字符 “HE”，H 对应的数字是 7，E 对应的数字是 4，这样就得到了一个二维向量 （这里假设n = 2）。

• 对于每一组由明文字符转换得到的向量P ，计算加密后的向量C = KP (mod 26) 。例如，若密钥矩阵 ，明文字符向量 ，那么加密后的向量C计算如下：

• 然后对向量中的每个元素进行模 26 运算，得到 

• 最后，将加密后的向量中的数字按照前面的转换规则，转换回字符。在上述例子中，15 对应的字符是 P，所以加密后的密文是 “PP”。按照这个方法，对所有分组后的明文进行加密，就得到了完整的密文。

• 首先，因为加密是通过C = KP(mod 26)进行的（其中C是密文向量，K是密钥矩阵，P是明文向量），所以解密需要用到密钥矩阵K的逆矩阵K^-1。

• 对于一个n * n 的密钥矩阵K，计算其在模 26 意义下的逆矩阵。计算逆矩阵的方法有多种，例如对于二阶矩阵 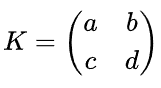，其逆矩阵（在普通实数范围内）是 。在模 26 运算中，需要先计算出ad - bc在模 26 下的乘法逆元。例如，如果ad - bc = 7，那么需要找到一个整数x使得 7x ≡ 1 (mod 26)，通过计算可以得到 x = 15（因为 7 * 15 = 105 ≡ 1 (mod 26)），然后再按照逆矩阵的形式计算出模 26 下的逆矩阵。

• 把密文按照加密时的分组方式，每 n 个字符一组进行划分。

• 对于每组密文字符，根据字母表顺序将其转换为数字向量。例如，A 对应 0，B 对应 1，……，Z 对应 25。假设密文是 “PP”，当  时，P 对应的数字是 15，所以密文向量是 。

• 对于每一个密文向量 C，计算明文向量 P = K^-1 C (mod 26)。例如，若密钥矩阵 K 的逆矩阵 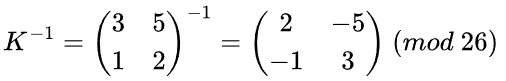（这里假设已经计算好了逆矩阵），密文向量 ，那么解密后的向量 P 计算如下：

• 然后对向量中的每个元素进行模 26 运算，得到 。

• 最后，将解密后的数字向量中的数字按照字母表顺序转换回字符。在上述例子中，7 对应的字符是 H，4 对应的字符是 E，从而得到明文。按照这个方法，对所有分组后的密文进行解密，就可以得到完整的明文。

注：鼎星安全有对此文章的修改和解释权。如欲转载或传播此文章，必须保证此文章的完整性，包括版权声明等全部内容。未经允许，不得任意修改或者增减此文章内容，不得以任何方式将其用于商业目的。