图神经网络系列一：图神经网络简介

一. GNN原理介绍

    图数据不规则，每个图的无序节点大小是可变的，且每个节点有不同数量的邻居节点，因此一些重要的操作如卷积能够在图像数据上轻易计算，但是不适用于图数据，可见图数据的复杂性给现有的机器学习算法带来了巨大的挑战 。

    此外，现有的机器学习算法假设数据之间是相互独立的，但是，图数据中每个节点都通过一些复杂的连接信息与其他邻居相关，这些连接信息用于捕获数据之间的相互依赖关系，包括：引用，关系，交互。

    近年来，人们对扩展基于图数据的深度学习越来越感兴趣。在深度学习的驱动下，研究人员借CNN,LSTM,深度AE的思想设计了图神经网络的架构。为了处理复杂的图数据，在过去几年中，对重要算子的泛化和定义发展越来越快。例如，图1说明了图卷积算子是如何受标准2-D卷积算子的启发的。

    图(Graph)是一种数据结构，常见的图结构模式包含图的节点(node)和边(edge)，其中边包含实体之间的关系(relationship)信息

传统的机器学习所用到的数据是欧氏空间(Euclidean Domain)的数据，欧氏空间下的数据最显著的特征就是有着规则的空间结构，比如图片是统一大小的长方形栅格，语音数据是一维序列，这些数据能够通过一维或二维的矩阵进行表示，进行卷积等操作较为高效。同时，存在一个核心的假设：样本之间是相互独立的。

但是，在现实生活中许多数据都是不具备规则的空间结构，在非欧氏空间下的数据，如电子交易、推荐系统等抽象出来的图谱，图谱中每个节点与其他节点的连接不是固定的。图神经网络可以对非欧氏空间的数据进行建模，捕获数据的内部依赖关系。

    图神经网络(Graph Neural Network)是不规则的、无序的，除了能够学习结构化数据(输出数据为图结构数据)之外，还能学习到非结构化数据，⽐如文本(texts)和图⽚(images)，并能够在提取出的图结构中进⾏推理(reasoning)，比如NLP的句法依赖树(dependency tree of sentences)和CV的场景图(scene graph of images)等都需要图推理模型

GNN本质上是⼀种连接模型，通过网络中节点之间的信息传递(message passing)的方式来获取图中的依存关系(dependence of graph)，GNN 通过从节点任意深度的邻居来更新该节点状态，这个状态能够表示状态信息

选择处理图的原因可以归纳为以下几点：

• 图提供了一种更好的方式来处理诸如关系和交互之类的抽象概念。它们还提供了直观的视觉方式来思考这些概念。图还构成了在社会环境中分析关系的自然基础。

• 图可以通过将问题简化为更简单的表示形式来解决更复杂的问题，或者从不同的角度将问题转换为表示形式。

• 图论和概念用于研究和建模社交网络，欺诈模式，功耗模式，病毒性以及在社交媒体中的影响力。社交网络分析（SNA）可能是图论在数据科学中最著名的应用。

• 标准的神经网络不能处理图结构输入，需要节点的特征按照一定的顺序进行排列，但是对于图结构而言并没有天然的顺序而言，GNN采用在每个节点上分别传播(propagate)的方式进行学习，由此忽略了节点的顺序，相当于GNN的输出会随着输入的不同而不同

• 图结构的边表示节点之间的依存关系，在传统的神经网络中，依存关系是通过节点特征表达出来的，无法显式地表达中这种依存关系。而GNN通过邻居节点的加权求和来更新节点的隐藏状态。

• 对于高级的AI来说，推理是一个非常重要的研究主题，人类大脑的推理过程基本上都是基于图的方式，这个图是从日常的生活经历中学习得到的。GNN尝试从非结构化数据比如场景图和故事文本中产生结构化的图，并通过这些图来生成更高级的AI系统

• 图卷积网络(Graph Convolutional Networks)和图注意力网络(Graph Attention Networks)，涉及到传播步骤(propagation step)

• 图的空域网络(Spatial-temporal Networks)，该模型通常用在动态图(Dynamic Graph)上

• 图的自编码(Auto-encoder)，该模型通常使用无监督学习(unsupervised)的方式

• 图生成网络(Generative networks)，为生成式网络

二. GNN模型概述

2.1 递归图神经网络

3.1 图卷积神经网络（GCN）

什么是GCN

GCN (图卷积神经网络) 就是将CV领域CNN的思想转移到图谱中。先回顾一下CNN的卷积结构：

可以简单理解为对每个像素点利用卷积核汇聚其邻居像素点的特征生成新的像素点。 但对于图谱来说，图中每个节点都有不同的出度和入度，即每个节点的结构都是独一无二的，因此传统的CNN、RNN在图上根本起不了作用。GCN采取的解决办法其实很容易理解，既然CNN是聚合像素点邻居的特征，那对于图谱就可以聚合每个节点和邻居节点的信息，CNN是利用卷积核进行信息的聚合，而GCN也设计了一个公式用于聚合图节点的邻居特征，这一个公式就是整个GCN的核心。

GCN中图节点的卷积 

以上大概就是GCN的核心思想，至于为什么这样的图卷积方法可行，我认为是基于一个假设：图中节点的状态始终受其周围节点的影响，节点距离越近，影响越大。

3. 什么是拉普拉斯矩阵？

拉普拉斯矩阵(Laplacian matrix) 主要应用在图论中，作为一个图的矩阵表示。对于图 G=(V,E)，其Laplacian 矩阵的定义为 L=D-A，其中 L 是Laplacian 矩阵， D=diag(d)是顶点的度矩阵（对角矩阵）,d=rowSum(A)，对角线上元素依次为各个顶点的度， A 是图的邻接矩阵。

频域卷积的前提条件是图必须是无向图，只考虑无向图，那么L就是对称矩阵。

3.1 常用的几种拉普拉斯矩阵

3.2 GCN 的模型结构

H代表每一层的特征，右上角的标号代表层数，如果是输入层，H就是输入特征X，维度为N*F，F为特征维度

sigmoid是激活函数

A波浪代表的是邻接矩阵A + I ，I代表单位矩阵

D带波浪代表的是A波浪的度量矩阵（degree matrix），是对角矩阵，每个元素代表该节点连接的节点数

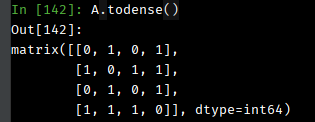
验证：

0.3333 * 1 + 0.2887 * 2 + 0.2887 * 1  = 1.1994

0.3333 * 2 + 0.2887 * 3 + 0.2887 * 4 = 2.6875

GCN 整体结构